Это действительно так, но всё же, если считать фотографию, лист бумаги, поверхность зеркала– двухмерными объектами, а тонкую проволоку, линию на бумаге – одномерными, то с равными на то правами существуют и четырёхмерные объекты – простейшие из которых – гиперкуб ( четырёхмерный куб ) и гиперсфера( четырёхмерная сфера ).<br><br >

Разведку боем! Сначала познакомимся с обитателями четвертого измерения.<br><br>
<strong>Четырехмерный куб.</strong><br><br>
Чтобы представить себе четырехмерный куб, полезно сначала посмотреть на обычный — трехмерный — куб, а также на «двумерный куб» (квадрат) и «одномерный куб» (отрезок)<br><br>
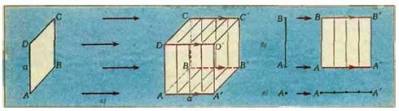
Смотрим на превращение одного в другое :<br>
<br>
Если точку «протащить» по бумаге, то получится линия. Линия, в свою очередь, «заметает» плоскость — получается квадрат. Вытянем квадрат из плоскости — сделаем куб. Это уже третье измерение.<br>
Но что же такое надо сделать с кубом, чтобы обратить его в четырехмерное тело? И как его себе представить? <br>
А что мы делаем, чтобы изобразить на плоском листе бумаги трехмерный куб? Мы проецируем его на плоскость. Получаются два квадрата один в другом, соединенные вершинами. Так спроецируем же и четырехмерный куб! Мы получим по аналогии два куба, один в другом, и снова вершины попарно соединены. Вот он, посланец четвертого измерения, вернее, не сам он, а его проекция на плоскость.<br>
<br>
Конечно, полученный чертеж четырехмерного куба условен, он дает его искаженное изображение. Но ведь и предыдущий рисунок трёхмерного куба дает искаженное изображение обычного куба на плоскости. <br>
На самом деле оба чертежа имеют одинаковую природу: они показывают образы трехмерного и четырехмерного кубов при параллельной проекции на плоскость. <br>
Разница лишь в том, что нам удается «Приподнять в пространство» плоское изображение трехмерного куба усилием мысли, а такой способностью представить себе «четырех-мерье» мы уже не обладаем.<br>
Ну, а если не удалось хорошо увидеть четырехмерный куб в движении — попробуем развернуть его. <br>
<strong><br>
Как его развернуть ? </strong><br>
<br>
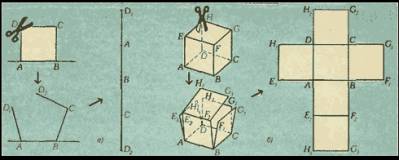
Чтобы представить себе развертку четырехмерного куба, сначала посмотрим на развертку трехмерного и двумерного кубов.<br>
<br>
<br>
<br>
<br>
<br>
<br>
<br>
<br>
<br>
<br>
<br>

Мы видим, что развертка квадрата одномерна и состоит из четырех отрезков; развертка куба двумерна и состоит из шести квадратов.<br>
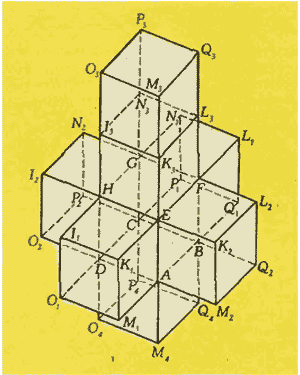
Аналогично, развертка четырехмерного куба трехмерна и состоит из восьми трехмерных кубов.<br>
<br>
Так же как трехмерный куб можно склеить из развертки, отождествляя вершины : G1 G2 и G3, а так жеН1,H2 и H3 (и соответствующие ребра), четырехмерный куб можно получить из его развертки, «склеивая» вершины, обозначенные одинаковыми буквами, но с разными номерами, например M1,M2,M3,M4 или I1,I2; при этом склеиваются не только вершины (и соответствующие ребра), но и двумерные грани, например М3O3P3Q3 и М4O4P4Q4. Разумеется сложить его можно только в четырёхмерном пространстве<br><br>
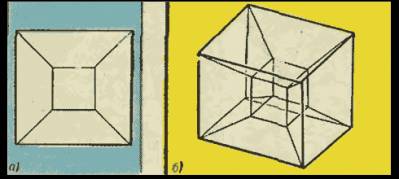
Существует еще один популярный способ изображения четырехмерного куба, представленный на рисунке.<br>
<br>
Восемь трехмерных граней изображены здесь внутренним (малым) кубом, внешним (большим) кубом и шестью усеченными пирамидами, соединяющими соответственные грани малого и большого кубов. Этот рисунок получается при центральном проектировании четырехмерного куба на некоторую «трехмерную плоскость». <br>
Смысл этого рисунка легче понять, если рассмотреть также рисунок (а), на котором изображена центральная проекция трехмерного куба на плоскость из некоторой точки. <br>
По рисунку удобнее всего сосчитать количество разного рода составляющих элементов четырехмерного куба. <br>
А именно, он имеет :16 вершин, 32 ребра, 24 двумерных грани (в виде квадратов) и 8 «трехмерных граней» (в виде кубов).<br>
<strong><br>
Попробуем познакомиться с другим представителем четырехмерного мира –гиперсферой.</strong><br>
<br>
Сфера нулевого измерения — это и есть точка. <br>
Нить, проволока и любая иная линия — это уже одномерные предметы: <br>
у них есть длина. <br>
Сфера в пространстве одного измерения — это две точки на прямой:<br>
центр этой одномерной сферы лежит посередине между ними. <br>
Представители двумерного мира имеют длину и ширину — это ленты, куски ткани, листы бумаги. <br>
Окружность, граница двумерного круга — вот что такое сфера в пространстве двух измерений. <br>
И наконец, кубы, пирамиды, дома, и мы с вами, входят в неисчислимую армию «трехмерцев», обладающих вдобавок к длине и ширине еще и высотой. У них есть объем. <br>
Сфера в трехмерном пространстве — это шар, «обычная» сфера. <br>
Но вот что любопытно: Проволоку можно сломать, лист бумаги разрезать, а куб распилить. И при этом получается, что одномерная поверхность, линия, разделяется поверхностью нулевого измерения — точкой. Двумерная плоскость делится надвое одномерной линией, а трехмерный куб — двумерной плоскостью. <strong>Иными словами, границей «разлома» тела служит какое-то другое тело, измерение которого на единицу ниже.</strong> <br>
Что же тогда служит границей четырехмерной сферы? <br>
Рассуждая по аналогии, мы можем отдаленно представить себе четырехмерную сферу.<br>
Если спроецировать глобус на плоскость, то проекции двух его половин наложатся одна на другую, и Нью-Йорк окажется где-то в центре Сибири. Проецируя глобус, мы пропускаем одну его полусферу сквозь другую и соединяем их проекции, круги, только по границе окружности (как квадраты по вершинам). Проекция гиперсферы — два шара, прошедшие один через другой и соединенные только по внешним поверхностям.<br>
Конечно, вообразить все это нелегко, но ничего мистического тут нет. <br>
Итак, знакомство состоялось. <br>
Так и хочется задать «четырехмерцам» традиционный вопрос: «Ну как там?» <br>
Но гиперкуб молчит всеми своими восьмьюдесятью элементами, и нам остается лишь еще раз прибегнуть к испытанному приему — разбежаться перед прыжком: раз надо исследовать свойства четвертого измерения — отступим пока во второе.<br>
<strong><br>
Я вам приведу отрывок из книги «Геометрическая рапсодия» :</strong><br>
<br>
Представьте себе некую сказочную двумерную страну – «Плоскатию», жители которой живут в плоском мире, и сами тоже двумерны. И вот в этот плоский, плоский, плоский мир является существо из третьего измерения — сфера. Квадратный житель Плоскатии увидел перед собой круг, который вел себя самым противоестественным образом: он то раздувался, то сжимался. Сколько ни пыталась Сфера объяснить Квадрату, что все эти видимые им круги разного диаметра — это все она одна, когда проходит сквозь Плоскатию вверх и вниз, он так и не сможет вообразить себе трехмерную сферу, пронизывающую его двумерный мир. Как можно убедить разумное существо, что ты посланец иных миров? Только продемонстрировав ему чудо. Здесь у нас с вами, как и у любого «трехмерца», самые широкие возможности. Ну что нам стоит вынуть плоскатика из его дома (а это просто замкнутая кривая), не разрушая стен? Извлечь содержимое плоского яйца, не протыкая его скорлупы? Да просто, наконец, приподнять любой предмет в этой стране над плоскостью и тем самым «выключить» его из жизни и даже из поля зрения? И пусть плоскатики сочиняют свои басни о своих «летающих тарелочках». Если две Плоскатии удалены друг от друга на тысячи световых лет, но плоская лента их мира извивается в пространстве так, что одни ее участки оказываются поблизости один от другого, то мы легко можем перенести плоскатика из одной галактики в другую со скоростью, в тысячи раз превышающей «его» скорость света: ведь мы пронесем его через третье измерение. Такие сказочные возможности несет в себе увеличение размерности мира всего на единицу. Это значит, что «четырехмерцы» так же всемогущи по отношению к нам, как мы — по отношению к «двумерцам».<br>
<strong><br>
А сейчас немного информации для размышления : </strong><br>
<br>
Дело в том, что мы сами живем в третьем измерении и поэтому смотрим на него «изнутри», наш объемный мир мы видим как бы плоским. Звучит парадоксально, но поместите лист бумаги с нарисованной на нем Плоскатией и всеми ее обитателями точно на уровне глаз — и вы на секунду испытаете трагедию плоскатиков, обреченных жить в двух измерениях, но ощущать лишь одно. Ведь чтобы увидеть фигуру — квадрат ли, круг, им надо хоть немного «выскочить» из своей плоскости. Но это невозможно, и именно поэтому весь мир они восприни­мают как прирывистую прямую линию. Остается лишь обойти фигуру со всех сторон и ощупать ее, что бы понять её форму. <br>
<strong><br>
Так ли мы с Вами ушли далеко от плоскатиков ?</strong><br>
<br>
Ровно на одно измерение!<br>
Вот простейший пример: Дана замкнутая кривая — круг или квадрат. Требуется чисто умозрительно, без карандаша и бумаги, решить: можно ли соединить две точки — одну внутри кривой, другую вне ее, но так, чтобы не пересечь замкнутой кривой. <br>
<br>
Перед тем как читать дальше, мысленно ответьте себе на этот вопрос!<br>
<br>
Представив себе этот элементарный чертежик и немного поразмыслив, мы уверенно утверждаем, что задача невыполнима. Это сработала нормативная функция воображения. Дело в том, что наш «внутренний взор» несет в себе евклидову плоскость — лист бумаги.<br>
Конечно же, на листе не соединишь две точки, не перечеркнув кривую, охватывающую одну из них. Но кто говорил нам о типе поверхности, на которой предстоит решать задачу? <br>
А если это не плоскость, а, скажем, бублик или автомобильная шина — все получается легко и просто. <br>
<br>
Человек слишком привык к двумерному миру. Наша «вообразительная» интуиция тут никогда нас не подводит. Но как только дело доходит до пространственных представлений, она начинает хромать. Высоту дома оценить куда труднее, чем его длину или ширину. А сказать, как далеко находится самолет или облако, неподготовленный человек не может даже приблизительно. <br>
Третьей координатой — не то что четвертой! — нам еще овладевать и овладевать. <br>
Причина тут не психологическая, а чисто физиологическая. Все дело в устройстве наших глаз. Когда мы смотрим на удаленный предмет, особые мускулы изгибают хрусталик глаза — естественную линзу, чтобы изменить ее фокусное расстояние и дать нам увидеть предмет отчетливо. Если же мускулы устали, то приходится заводить очки и менять фокусное расстояние искусственно. Наводка на резкость фотокамеры — полная аналогия этому процессу, который в физиологии называется аккомодацией. <br>
И еще в каждом глазе есть группа из шести мускулов, которые поворачивают его таким образом, чтобы направления взгляда правого и левого глаза пересекались в одной точке. Это называется конвергенцией. Так создается бинокулярный эффект — мы видим мир объемным. Стереоскоп, в котором рассматривают «выпуклые» картинки, построен по этому же принципу.<br>
«ТРЕТЬЕ ИЗМЕРЕНИЕ МЫ ОБНАРУЖИВАЕМ С ПОМОЩЬЮ АККОМОДАЦИИ И КОНВЕРГЕНЦИИ. ВОСПРИЯТИЕ ТРЕТЬЕГО ИЗМЕРЕНИЯ СВОДИТСЯ К ОЩУ­ЩЕНИЮ УСИЛИЯ, КОТОРОЕ МЫ ИСПЫТЫВАЕМ ПРИ АККОМОДАЦИИ КАЖДОГО ГЛАЗА, И ОЩУЩЕНИЮ УСИЛИЯ, КОТОРОЕ ВОЗНИКАЕТ В ОБОИХ ГЛАЗАХ, КОГДА ОНИ НАСТРАИВАЮТСЯ НА НУЖНЫЙ УГОЛ СХОДИМОСТИ — ТО ЕСТЬ ПРИ ИХ КОНВЕРГЕНЦИИ. ОБА ЭТИ ОЩУЩЕНИЯ МУСКУЛЬНЫЕ, ОНИ СОВЕРШЕННО НЕ ПОХОЖИ НА ЗРИТЕЛЬНЫЕ ОЩУЩЕНИЯ, КОТОРЫЕ ПОЗВОЛЯЮТ НАМ ВОСПРИНИМАТЬ ПЕРВОЕ И ВТОРОЕ ИЗМЕРЕНИЯ»,<br>
<strong>— это пишет не физиолог, а математик, притом известнейший — Анри Пуанкаре.</strong><br>
<br>
Впрочем, любой из нас сам мог бы прийти к подобным выводам на основе собственного опыта. Мы видим плоскую картину, улавливаем игру света и тени, краски, взаимное расположение фигур и цветовых пятен на ней — и все это зрительные ощущения. Панорама же требует от наших глаз включить мускульный аппарат аккомодации и конвергенции, и <em>мы </em>мгновенно <em>ощущаем </em>его работу. Но интуиция на мускульные усилия, как и на пространственное расположение фигур, у человека не выработалась. <br>
Не такой уж это простой вопрос о том, как мы видим пространство. <br>
И в самом деле, мы живем в трехмерном мире, а мысль наша между тем издавна привержена к двум измерениям. <br>
Ещё 500 лет назад люди думали что земля – плоская.( Галилео Галилей, Джордано Бруно, Коперник – это 16-17 век.)<br>
Человечество пошло не по пути овладения третьим измерением, а по пути его «приручения»: люди старались втиснуть объем в плоскость, изобразить окружающий мир на скале, песке или папирусе. <br>
<strong><br />
Дальше больше !<br>
Немного о вселенной.</strong><br>
<br>
Вселенная бесконечна? Но что же тогда за ее краем? <br>
Альберт Эйнштейн нашел выход из этого логического тупика.<br>
Вселенная хотя и конечна, но безгранична! С ней как раз все в порядке. Беда в нас самих — в нашей слепой приверженности к геометрии Евклида. Мы уверены, что параллельные линии не пересекаются, что кратчайшее расстояние между двумя точками — прямая. Но ведь этого никто и никогда не доказал. Мало того, все мы знаем, что это вовсе не так. Чтобы сократить дорогу от Москвы до Владивостока, летчик поведет самолет вовсе не по прямой линии, а по дуге большого круга Земли — так называемой геодезической линии. Если нарисовать на земной поверхности огромный круг, то отношение его диаметра к длине окружности будет меньше <em>Пи. </em>Все это из-за кривизны нашей планеты, из-за того, что она не плоская. Параллельные линии — дуги большого круга — пересекаются. И узнали мы об этом задолго до космических полетов, людям не пришлось глядеть на свою планету извне, чтобы понять, какой она формы. <br>
Так и Эйнштейн, размышляя над известными астрономическими фактами, пришел к мысли, что наша Вселенная искривляется и в математическом смысле эквивалентна четырехмерной сфере <br>
Тут полная аналогия с Плоскатией, расположенной на поверхности большого шара, которая тоже искривляется в пространстве, но высшем (трехмерном), чем то, что могут осознать плоские «двумерцы». <br>
Плоские «двумерцы», живущие на сфере, смогли бы обнаружить, что их вселенная искривлена, если бы стали, например, строить заборы вокруг какого-нибудь своего дворца ( вместо заборов могут быть любые концентрические окружности ) — один за другим, каждый длиннее предыдущего. В один прекрасный момент они бы обнаружили, что на новые заборы идет все меньше материала. Какой-нибудь гениальный плоскатик сообразил бы, что строители перешли за экватор сферы. <br>
Нам, «трехмерцам», пришлось бы строить гигантские сферы вокруг Земли — одну больше другой.<br>
Разговоры о «Плоскатиках» могут показаться детскими забавами. <br>
Если вам так кажется, то проведите такой эксперимент: <br>
Вы, вероятнее всего, сейчас сидите за столом. <br>
Наклоните голову над столом как можно ниже, начинайте смотреть в стол, и мысленно расположите себя на его поверхности - в двух измерениях. <br>
А теперь представьте : какое может быть мировосприятие у Этого существа ? Ведь Оно будет основано только на той информации, которую Существо видит вокруг.<br>
Может показаться, что с нами всё по другому…<br>
Однако давайте смотрите: <br>
Собаки видят мир в двух цветах, а ведь это не значит что он действительно такой.<br>
Муравей ощущает только 2 измерения ( будь он наделён интеллектом человека, он всё равно не смог бы понять, что Земля - круглая ). <br>
Мир для микроба - совсем иной.<br>
Представьте себя на миг одним из этих обитателей планеты, и вам станет ясно, почему мы не можем понять строения вселенной.<br>
Человек - "Венец природы" - почему то думает, что Его мировосприятие - единственно правильно. Он пытается втиснуть законы Вселенной в законы физики, а законы эти, мягко говоря, не блещут. <br>
Эвклидова геометрия - хороша на листе бумаги, а вот в трёх измерениях, увы, хромает. <br>
Теорема Пифагора не действует на геоиде - которым является наша планета.<br>
В заключение добавлю : Альберт Эйнштейн - это гений, или просто дурачёк с высунутым языком, но глубина его фразы действительно заслуживает уважения : <br>
"ВСЁ ОТНОСИТЕЛЬНО - ГОСПОДА"</p>
Если вам интересно почитать про одностороннюю бесконечную поверхность , которую можно подержать в руках, про мистическое «Золотое сечение», посмеяться с анекдотов, вникнуть в глобальные мысли философов ( цитаты ) – тогда заходите на сайт : <a href="http://sozercaem.com.ua/" class="links" target="_blank">SOZERCAEM.COM.UA</a>
-с которого и были предоставлены материалы

Источник: http://sozercaem.com.ua/